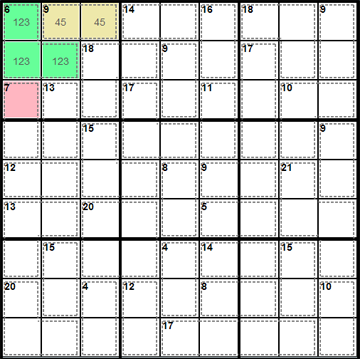
Killer Sudoku Walkthrough

Look at the cells shaded yellow on the right. As you can see, they each are the last unknown cell of a cage, so we can immediately calculate their value.

Now look at the cage shaded in green. The possible combinations of 14 are 5,9 or 6,8. But, because there is already a 6 in the block, the only possible combination left is 5,9. Now there already is a 5 in column 6, therefore the rightmost cell of the cage must be the 9 leaving the other cell to be a 5.

Most of the rest of this "Easy" graded puzzle can be solved using the strategies just applied.

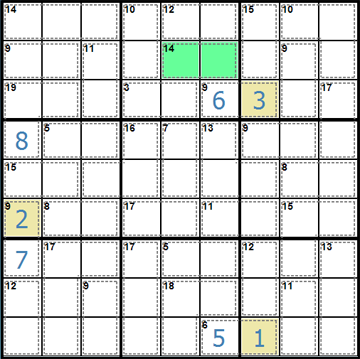
Now, let us look at a more difficult situation that you may need to start this "Hard" puzzle to the right.

Another useful starting point is to look for all cages that can only have one combination of numbers. For two-cell cages, the totals 3, 4, 16 and 17 only have one combination, for three-cell cages, 6, 7, 23 and 24 have one combination, for four-cell cages, 10, 11, 29 and 30 have one combination and for five-cell cages, 15, 16, 34 and 35 have one combination.

Looking at the cage shaded green, the only possible combination of three cells adding to 6 is 1,2,3. Therefore we know that those 3 cells will use the numbers 1,2,3. The cage shaded yellow has a number of combinations making 9 but we cannot use any combination that contains a 1, 2 or 3 as those are taken by the green cage. Therefore the only combination left for the yellow cells is 4,5.

Now the highlighted cell (shaded pink) cannot contain a 1,2,3,4 or 5 as all are used in the same block. Therefore, for the cage to total 7, the only possible combination left is 1,6 and so that cell must be a 6.

This should be enough information to get you solving. Good luck.