DKM Yubotu Help

Object of the Puzzle

In order to successfully complete the puzzle, you need to place all the ships in the fleet in their correct positions in the grid. There are four puzzle options:

• A ten ship fleet consisting of one battleship (four squares in length), two cruisers (three squares in length), three destroyers (two squares in length) and four submarines (one square each). This fleet is placed in a 10x10 grid.
• A fifteen ship fleet consisting of one aircraft carrier (five squares in length), two battleships, three cruisers, four destroyers and five submarines. This fleet is placed in a 12x12 grid.
• A twenty ship fleet consisting of two aircraft carriers (five squares in length), three battleships, four cruisers, five destroyers and six submarines. This fleet is placed in a 14x14 grid.
• A twenty five ship fleet consisting of three aircraft carriers (five squares in length), four battleships, five cruisers, six destroyers and seven submarines. This fleet is placed in a 16x16 grid. (Not available in phone version.)

The ships are placed either horizontally or vertically in the grid but no two ships may occupy adjacent grid squares, even diagonally. All other squares must be occupied by water.

At the start of a new puzzle, you are give one or more squares already filled in. These may be ship segments or water. All the other squares are "unknown". To help you solve the puzzle, you are also shown the number of ship segments contained in each row and column (numbers down the right and the bottom of the grid).

How To Play

• Click the "New" button to get a puzzle. There is a new one available every day at each difficulty level for each fleet size.
• Identify a square that you have determined it's contents and select the appropriate icon from the toolbar (if not already selected). The mouse cursor will change to the selected icon. Then click on the square to set the contents. For details of the toolbar icons, see below.
• You can change the currently selected icon by using the mouse wheel to scroll up/down through the list of icons.
• Another way to quickly set the selected icon is to use the keyboard -
  W or Space key for Water
  Delete key for eraser
  or 0 for Eraser, 1 for Water, 2 for Submarine, 3 for Left Segment ...
• To undo a move, click the "Undo" icon. You can undo all the way back to the beginning.
• To check your input, click the "Tick" icon and any incorrect squares will be marked with a red cross.
• If you have filled in unknown segments and it is now obvious what part of a ship each segment is, you can quickly convert unknown segments but selecting the "Convert Segments" option in the Edit menu.
• If you are stuck, you can get a hint by selecting the "Hint" menu option (under "Solve"). At any point in time, at least one of the squares will be able to be solved by logic alone.
• If you require more help, select the "Solve One Cell" menu option (under "Solve"). This will fill in a square (cell) and give you the reason for that value.

Toolbar Icons

	Fills a square with water.
	Fills a square with a submarine.
	Fills a square with the left segment of a ship.
	Fills a square with the right segment of a ship.
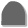	Fills a square with the top segment of a ship.
	Fills a square with the bottom segment of a ship.
	Fills a square with the middle segment of a battleship or cruiser.
	Fills a square with a yet to be determined segment of a ship. Use this when you know the square must contain a ship segment (or submarine) but you do not know which yet.
	Fills all empty squares in a row with water. (Shortcut to entering water multiple times)
	Fills all empty squares in a column with water.
	Clears a square.

Solving Strategies

There are three basic solving strategies for these Yubotu puzzles. All the beginner puzzles can be solved with just these strategies alone. Of course, there are more advanced strategies but they are not covered in this help.

A useful learning tool is the "Solve One Cell" menu option. It will fill in a cell for you and give you the reason why it needs to be that value.

The three basic strategies are:

1. Fill in what you know about squares adjacent to ship segments.
2. Fill up rows and columns with water when all the ship segments for that row/column are known.
3. Fill in ship segments in rows/columns when all their remaining spaces must be a ship to equal number for that row or column.

In all explanations below, a square in row i, column j will be referred to as (i,j) - for example, row 3 column 4 will be (3,4).

Consider the following puzzle:
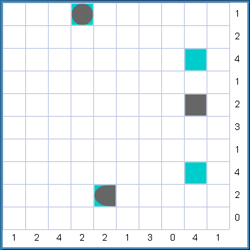	Using strategy 1, we know that all ships are surrounded by water, therefore we can fill in water for (1,3) (1,5) (2,3) (2,4) (2,5) around the submarine at (1,4). Now, consider the left ship segment at (9,5). (9,6) must be the remainder of a destroyer because that row only contains two ship segments. So we can complete this ship and then surround it with water. Now look at the middle segment at (5,9) where we can place a ship segment either side of it. You can see that the ship must be vertical because the column to the left of it does not contain any ship segments. So we can place a top segment at (4,9) and an unknown segment at (6,9) as we don't yet know whether this is a cruiser or a battleship. We can then fill in water at (3,8) (3,10) (4,8) (4,10) (5,8) (5,10) (6,8) (6,10) (7,8) and (7,10). Using strategy 2, we can fill the remainder of row 9 with water as all ship segments are known. (Tip: Use the icon to do this with one click.) We can also fill in row 1, row 4, row 10, column 6 and column 8 with water because all ship segments in those rows and columns are known.
The puzzle now looks like this:
	Now look at row 8. There are four ship segments required and only four empty spaces. So, using strategy 3, we can fill in the cruiser and submarine in that row. After adding water around these ships, we see that the ship segment at (6,9) must be the bottom of a cruiser, so we can convert it. Again, using strategy 3, we can now fill in a ship segment at (2,9) completing the four ship segments required by column 9. We can also fill water in column 1 and column 10 because all ship segments are known. This means that (2,9) can be changed to a submarine.
The puzzle now looks like this:
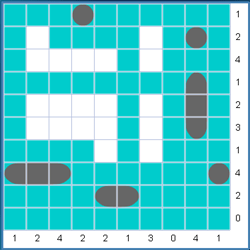	Time to introduce a new strategy. Sometimes it is useful to see where the longest ship can be placed, in this case the battleship. If you look carefully, you will see that the only place it can fit is row 3. After placing it, we can now fill in water at (2,2) (3,7) and can fill columns 2, 4 and 5 with water. There are now only two spaces in column 3 for the remaining 2 ship segments so we can place a destroyer in (5,3) and (6,3). Using basic strategies, we can easily fill in the remaining two ships giving final solution below:
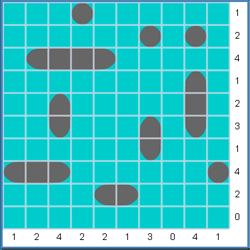	This should be enough to get you going. Good luck!