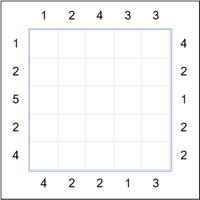On the left is a 5x5 grid Towers puzzle. The objective is to fill in all the empty cells such that each row and column contains numbers 1 to the size of the group, in this case 5. Each number represents a tower of that height and the clue numbers on the sides tell you how many towers are visible from that direction. Higher towers obscure any lower than them.
Let's start.

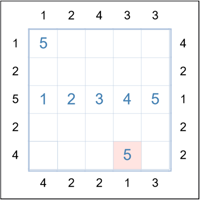The easiest place to start is to look for clue numbers 1 and 5 (size of grid). You will see that on the left of row 3 is a 5. So the only way to see 5 "towers" is to place the number 1,2,3,4 and 5 in that sequence in that row. Also, wherever there is a 1 clue, the first cell from that clue must be the 5 (max number).
The grid to the left has these values filled in.

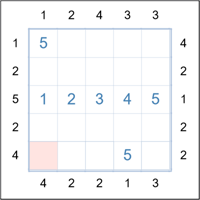Now consider the highlighted cell in the bottom left. It can only contain a 2, 3 or 4. However, because 4 towers must be viewable (clue at left of row 5), the first cell cannot be a 3 or 4 if there are to be 4 towers visible. So the cell must be a 2.

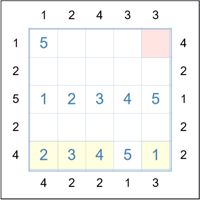It follows that the next two cells in that last row are 3 and then 4 and we can then fill the last cell in that row with a 1. (Yellow cells to the left.)
Look now at the top right cell. As before it can only contain a 2, 3 or 4 and because 4 towers must be viewable for the top row looking from the right, the highlighted cell cannot be a 3 or 4. So the cell must be a 2.

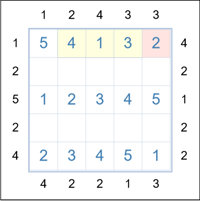The remaining numbers for the top row are 1, 3 and 4 but because column 3 already contains a 3 and 4, the 1 must go in that column. The 4 then goes in column 2 and the 3 in column 4. (Yellow cells to the left.)

 

Now consider the two missing cells in column 1. They contain a 3 and 4 and the only way they can fit to satisfy the 4 clue at the bottom is for the 3 to be in row 4 and the 4 in row 2. (See yellow cells below.)

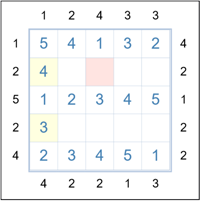Look at the pink highlighted cell. For column 3 it must be a 2 or 5. But in order to satisfy the 4 clue at the top of the column, the cell must be a 2.
All remaining cells can now be solved by the basic rule of finding the one place in each row/column that does not have the number already.

 

This was an easy puzzle but should get you started. You will discover new techniques as you play more. If stuck you can use the "Solve One Cell" option. (See help for more on that subject.)