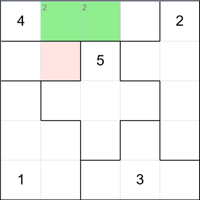On the left is a more advanced 5x5 grid Suguru puzzle that is trickier to solve.
Consider the top group of four cells. The 2 must go in one of the two green cells.
Now look at the highlighted cell. It belongs in a group of two cells and so must contain a 1 or a 2. But because one of the green adjacent cells must contain a 2, this cell cannot be a 2. We don't know at this point which green cell is a 2 but either one will invalidate the highlighted cell from being a 2. Therefore it must be a 1.

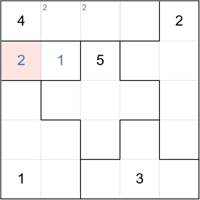The above demonstrates a fundamental principal in solving advanced puzzles.
Look for all cells in a group where a number can appear and any cell adjacent to ALL those cells cannot have that number.
This principal will be repeatedly demonstrated in this walkthrough.
Note that we have filled in the 1 and 2 of the two cell group. Smaller groups are easiest to work with initially.

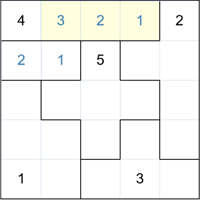We can now easily fill in the remaining numbers in the top group (shown in yellow).

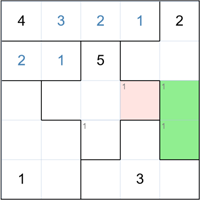Looking at the group on the top right, we can only two cells where the number 1 can appear (shown in green). In the middle cross-shaped group, there are also two places the 1 can go. But the highlighted cell is adjacent to both the green cells, therefore it cannot be a 1. This leaves only one place left for the 1 in the cross-shaped group.

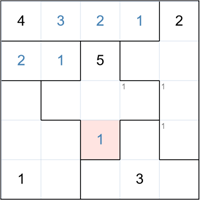Here we have filled in the 1 (highlighted cell). Another demonstration of the principle mentioned above.

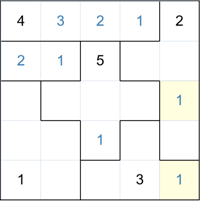We can now easily fill in two more 1's as there is only one place for them in their respective groups (shown in yellow).

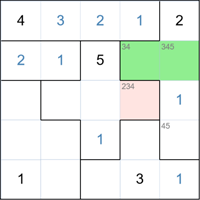Now back to the group on the top right. There are two cells where the 3 can go - shown in green. The highlighted cell can contain a 2, 3 or 4. But because it is adjacent to both the green cells and one of them is a 3, we can remove 3 as a possible.

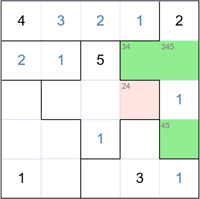In the group on the top right there are three cells where the 4 can go - shown in green. The highlighted cell is adjacent to all three green cells and as one of them must be a 4, we cen now remove the 4 from the highlighted cell. This means it must be a 2.

The rest of the puzzle can now be solved using basic techniques.

Hopefully this has given you enough to solve the difficult puzzles and some of them can be very tough! We have attempted to give a rating to the hard and tough puzzles on this site. It may be very useful to use some of the solve options offered. The option "Basic Possibles" will fill in all possibles just using basic elimination and you can use this as a start to spot the next cell to solve.